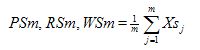|
Specification
Feature Parameters
Feature Parameters
According to ISO 4287-1997[4], feature parameters are based on the three concepts of profile peak, profile valley, and profile element. These are accordingly defined in this standard as:
Profile peak
An outwardly directed (from material to surrounding medium) portion of the assessed profile connecting two adjacent points of the profile with the X-axis.
Profile valley
An inwardly directed (from surrounding medium to material) portion of the assessed profile connecting two adjacent points of the profile with the X-axis.
Profile element
Profile peak and the adjacent profile valley.
Note: The positive or negative portion of the assessed profile at the beginning or end of the sample length should always be considered as a profile peak or profile valley. When determining a number of profile elements over several successive sampling lengths the peaks and valleys of the assessed profile at the beginning or end of each sampling length are taken into account once only at the beginning of each sampling length.
The note gives a method to deal with end effects and allocation of features to particular cut-offs that inevitably occur with profile feature parameters.
Also in this standard is an attempt to deal with insignificant features with the following:
Height and/or spacing discrimination
Minimum height and maximum spacing of profile peaks and profile valleys of the assessed profile which should be taken into account.
Note: The minimum height of the profile peaks and valleys are usually specified as a percentage of Pz, Rz, Wz or another amplitude parameter and the minimum spacing as a percentage of the sampling length.
Typically the minimum height discrimination is set as 10% of Pz, Rz, Wz and minimum spacing discrimination is set as 1% of the sampling length. The height and spacing discrimination, as stated in this standard, is ambiguous with many different interpretations.
The commonest interpretation of minimum height discrimination used in practice is based on up and down crossings. For a given height discrimination, 2H say, take two straight lines, one at height H above and parallel to the mean line, and the other at H below and parallel to the mean line. Traversing along the profile from left to right, an up-crossing is defined at an upward crossing of the upper parallel line and a down-crossing is defined as a downward crossing of the lower parallel line. Starting at the left end of the profile and traversing along the profile from left to right, mark the first up-crossing/down crossing. Then continue alternatively from a marked up-crossing marking the next down-crossing or from a marked down-crossing marking the next up-crossing, until the end of the profile is reached. The profile peaks at 2H height discrimination are defined as the portions of the profile between a marked up-crossing on the right and a marked down crossing on the left. The profile valleys at 2H-height discrimination are defined as the portions of the profile between a marked down-crossing on the right and a marked up-crossing on the left.
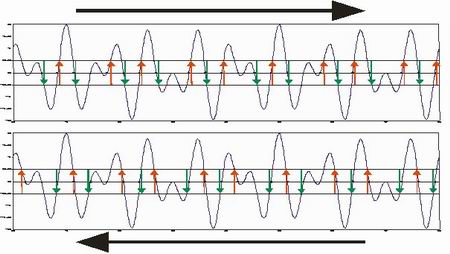
Figure 1 Different directions produced different marked crossings
(up-crossing red, down-crossing green).
This approach has one severe problem, if the profile is reversed in direction, different up and down crossing could be marked (see Figure 1). This leads to the philosophical problem of "are the identified features genuine features of the profile?” With the difference in results when the profile is reversed, the answer is clearly NO.
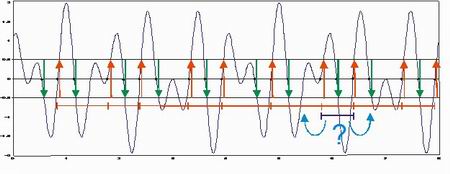
Figure 2 Which direction is an insignificant profile element combined?
Analysing the above algorithm, if the height discrimination is set to zero then all up and down crossings are through the mean line. As the height discrimination is gradually increased, adjacent pairs of up/down crossings, corresponding to profile elements insignificant at the given height discrimination, will be eliminated. The difference in results when the profile is reversed is caused by the direction in which these insignificant profile elements are combined to adjacent profile elements. When traversing from left to right they are always combined with the left profile element and when traversing from right to left they are always combined with the right profile element. What is required is a way of choosing which direction to combine insignificant profile elements independent of the direction of traverse (see Figure 2). Using concepts from pattern analysis (Scott 2004)[9] the following algorithm achieves this aim and is the one recommended.
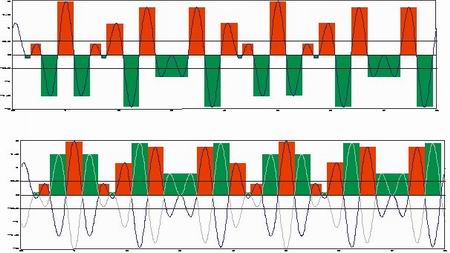
Figure 3 Portions above mean line are marked red, portions below green;
the below portions are then reflected about the mean line.
For either height discrimination, 2H say, or spacing discrimination S, mark all portions of the profile above the mean line with one colour and all portions of the mean line below with another colour. The segments of the profile below the mean line are then reflected about the mean line so they are now above the mean line (see Figure 3).
Find the smallest segment (for height discrimination this is the smallest in height, for spacing discrimination this is the smallest width). If the smallest segment is lower than the discrimination level (H for height, S for spacing), combine it with its two adjacent neighbouring segments so they become one segment at the same height as the largest neighbour (see figure 4). If the smallest segment is at the end of the profile discard it. If there are two or more smallest segments then start with the segments that were originally below the mean line (green segments); otherwise it does not matter what order they are processed. Continue until all segments are above the discrimination level (height or spacing).
The segments left are the required segments after either height or spacing discrimination.
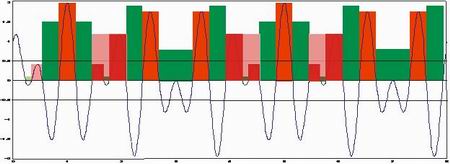
Figure 4 Start with smallest segments and combine with two adjacent segments,
If the smallest segment is at an end just remove the segment.
Feature Parameters
Name |
|
Type |
Feature Parameter |
Calculated from |
Roughness Profile |
Description |
Mean height of profile elements of the assessed profile
Pc, Rc, Wc
Mean value of the profile element heights Zt within a sampling length |
Mathematical |
With m profile elements in sampling length l
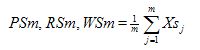
where Ztj is the height of the jth profile element within the sampling length and l = lp, lr or lw according to the case.
|
Graphic |
|
Source |
ISO 4287 – 1996 section 4.1.4 |
|
Use a natural cubic spline to interpolate through the discrete data values.
For each sample length,. determine portions of the profile above the mean line, these are the profile peaks and portions of the profile below the mean line, these are the profile valleys. Use the height discrimination algorithm, recommended above, at 10% of Rz to eliminate insignificant profile elements. Use the spacing discrimination algorithm, recommended above, at 1% of lr to eliminate insignificant profile elements.
For the evaluation length:
If an even number 2m of profile peaks and profile valleys
Calculate
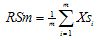
where Zti is the height of the ith profile element.
If an odd number of profile peaks and profile valleys
Rc is the mean of the two even segment calculations of Rc, one with the first segment after combination removed and the second with the last segment after combination removed.
|
Other Information |
The algorithm here is for the evaluation length and not for the mean of sampling lengths as defined in ISO 4287-1996, since this latter definition is metrologically unstable. |
Name |
|
Type |
Feature Parameter |
Calculated from |
Roughness Profile |
Description |
Mean width of profile elements of the assessed profile
PSm, RSm, WSm
Mean value of the profile element widths Xs within a sampling length |
Mathematical |
With m profile elements in sampling length l
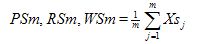
where Xsj is the width of the jth profile element within the sampling length and l = lp, lr or lw according to the case. |
Graphic |
|
Source |
ISO 4287 – 1996 section 4.3.1 |
|
Use a natural cubic spline to interpolate through the discrete data values.
For each sample length, determine portions of the profile above the mean line, these are the profile peaks and portions of the profile below the mean line, these are the profile valleys. Use the height discrimination algorithm, recommended above, at 10% of Rz to eliminate insignificant profile elements. Use the spacing discrimination algorithm, recommended above, at 1% of lr to eliminate insignificant profile elements.
For the evaluation length:
If an even number 2m of profile peaks and profile valleys
Calculate
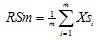
where Xsi is the width of the ith profile element.
If an odd number of profile peaks and profile valleys
RSm is the mean of the two even segment calculations of RSm, one with the first segment after combination removed and the second with the last segment after combination removed.
|
Other Information |
The algorithm here is for the evaluation length an not for the mean of sampling lengths as defined in ISO 4287-1996, since this latter definition is metrologically unstable. |
|