Underwater Acoustics

Acoustic reverberation occurs as sound is reflected, and such echoes can confuse the measurements. Without reverberation the sound energy from any one source flows away, giving a simple linkage between the energy flow (intensity), the acoustic pressure and the specific acoustic impedance.

However, in some circumstances, reverberation can be used to advantage, due to its capability to create a sound field in which energy is travelling in all directions. White noise generated in a highly reverberant tank can give pressure spectral level (PSL) which is almost uniform over the tank volume. The response of a hydrophone to such an environment gives an average over all directions without the need to conduct a multiplicity of tests.

Equally, when testing sources of wide band noise, these properties allow the source properties to be averaged over all directions.

However, a clear understanding of the background physics is necessary to be able to use such results in other conditions. Most environments fulfil neither extreme of zero or full reverberation, but nevertheless these ideals are useful for test purposes.

The reverberant pressure spectrum P_r provides the integration over all angles of the source, thus linking this to the total power spectral output W in the same band in Watts/Hz:

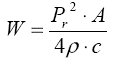Here, A is the effective area of loss of the tank in m². This has an analogy to the corresponding loss areas in a concert hall or reverberant air chamber, sometimes called metric Sabins (after Sabine, the pioneer of such work).

The units can again be shown to match. The units of the specific acoustic impedance in the denominator are kg/(m²s), whilst the numerator dimensions are N²/m², giving a quotient in N²s/kg. This reduces to Nm/s or watts as anticipated, by noting that a Newton force, N, has units kgm/s².

The area A can be determined, either by finding the decay time, as originally discussed by Sabine, or by plotting the variation of P² against the inverse range squared (1/r²) of a source, as the range r between source and hydrophone is changed. This is most simply presented using the source output S to give the equation:

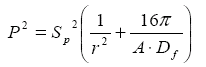The hydrophone must follow a track which starts from the effective centre of the source, to keep a constant value for its output S.

This straight line of P² against 1/r² is found for the higher frequencies where a uniformly omnidirectional reverberant field exists within the tank, where D_f is the directivity factor of the source in the direction of the traverse line followed (see directionality). This technique also allows S to be determined.