Underwater Acoustics

When the source is directional, the output differs in one direction from another. The directionality can be measured by rotating the source about a convenient axis, usually held orthogonal to the direction of measurement of the source output S (pressure range product P·r), i.e. the direction to the hydrophone.

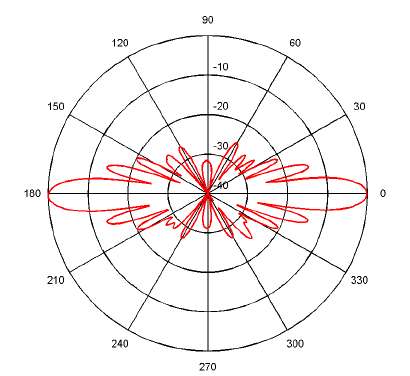The distribution of the source output with direction can then be plotted as a function of angle, to give a polar plot. The example above shows two main beams in opposite directions, and a set of side lobes at reduced levels. There are four shown at –13dB (intensity reduced by a factor 20), plus others at lower levels, separated by interference nulls.

The directivity and total output power can be determined by an integration over all directions, but this requires more data than can be shown in this two dimensional plot. However, the example shown has (approximate) mirror symmetry, and the full data set would show its symmetry about the rotational axis =0 (but not about =90°). The response then depends only on the angle shown, independent of the angle , measured in the plane orthogonal to the axis =0° (spherical polar angles).

The variation of source output provides a measure of directivity. The directivity factor D_f, in a specified direction ', , is the ratio of the source output in that direction to the average over all directions. Note that this integration must use the source output S, not the decibel source level SL.

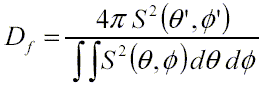The integration is made over a set of infinitesimal cones into which the sound propagates, each of which intercepts an area A of the spherical surface defined by a constant range r. The dimensionless ratio A/r² is a solid angle measured in steradians (sr). A solid angle including all directions has 4π steradians, to give a unity D_f for an omnidirectional source, typified by a simple source, where S is independent of direction.

The intensity at the hydrophone is given by:

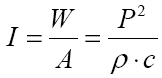so that

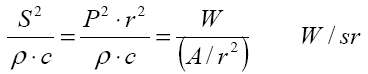Thus a plot of source output squared S² is an indication of the power per unit solid angle in watts per steradian, just as the sound pressure squared indicates the intensity. In both cases, the fluid properties are considered independent of position or direction.

The directivity index DI, is the sonar equation version:

Note that this is in dB with no reference since D_f is a power ratio. The polar plot gives data in dB, as the variation of DI with the specified direction. DI is particularly useful for calculation of the signal to noise ratio.