Calculation of absorption of sound in seawater

The equation for the seawater absorption coefficient at frequency f (kHz) can be written as the sum of chemical relaxation processes and absorption from pure water:

Total absorption	=	Boric Acid Contribution	+	Magnesium Sulphate Contribution	+	Pure Water Contribution

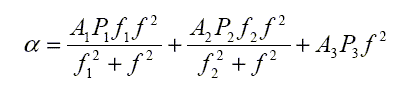
where the pressure dependencies are given by P₁, P₂ and P₃, and the relaxation frequencies are f₁ and f₂.

Whilst the physics underlying the absorption of sound by seawater has become more securely based with time, there remains scope for further improvements in the data quality and in the best method of presentation. All published algorithms are fitted to data of variable quality, so there can be no perfect answer. Particularly at low frequencies, the absorption in standard seawater is so small that immense quantities of such water are required to create measurable losses of sound energy into heat. These are difficult to separate from the spreading losses which occur as the sound wave propagates away from the source. The rate of this dissipation in the open ocean depends on the environmental conditions, and the quality of the data is thus dependent on the extent to which these are known. The use of sound ducts has proved useful to minimise the spreading losses, but this does create other sources of uncertainty.

There are laboratory alternatives, which include the use of artificially concentrated solutions, and resonator measurements to reflect the sounds back and forth through the same media. Many techniques have thus contributed to the current knowledge.

The work of Francois and Garrison (F&G), published in 1982, drew together a wide range of previous measurements including the earlier publication of Fisher & Simmons (F&S) in 1977. Further analysis was made by Ainslie and McColm (A&M) and published in 1997, but is based on the same data set. They showed that their simpler formula retained a similar accuracy of fit, and therefore invoked "Occam's razor" to suggest that their equations are preferable, at least in so far as they provide a simpler physical understanding. Where there are competing explanations, it is generally accepted that the simpler is to be preferred. When this simplicity requires making fewer assumptions, the heuristic maxim attributed to William of Ockham (or Occam) also implies that the simpler theory is more likely to be correct. William was a 14th century philosopher, and his principle is thus weaker than those based on more deterministic tests and measurements.

However, being simpler to describe, we base the description below on the equations of Ainslie and McColm.

Mechanisms of absorption

Viscous absorption generated by particle motion

For frequencies above 100 kHz, the particle motions generated by the sound produce heat via viscous drag. The absorption converts a proportion of the vibrational energy into heat as it travels through each successive specified distance (metres, kilometres, etc). This proportional loss gives an exponential decay which can be specified by a ratio, or more usually by the logarithm of this ratio presented in decibels. So the results for the absorption coefficient α are usually given in dB/km for the results of measurements of attenuation at sea. An absorption of 1 dB/km means that the energy is reduced by 21 % in each successive kilometre.

The coefficient α is found to increase with the square of the frequency f, so at frequencies greater than 1 MHz, results are usually given in dB/m, since the sound levels fall so rapidly. Such high frequencies are used at sea, for instruments such as direct reading sound speed meters, and Acoustic Doppler Current Profilers, but most marine applications of acoustics utilise much lower frequencies.

The coefficient α depends on the sea temperature T (here in °C) and the pressure or depth. Whilst the conversion between pressure and depth itself depends somewhat on other parameters, these effects are small compared with the overall errors and so the use of depth D in kilometres is often used for convenience to calculate the hydrostatic pressure. A simple conversion uses a fixed surface density of 1030 kg/m³, but this can be extended using a value for the bulk modulus of 2.32 GPa, to cover the increase in density with depth.

Ainslie & McColm then give, for viscous absorption, α as a function of f, T and D.

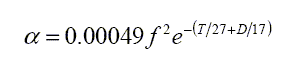
dB/km

This is a very small effect at audible frequencies, but dominant for frequencies greater than 1 MHz. Note that increases in temperature or depth decrease the absorption due to the negative exponential term shown.

The alternative equation given by F&G has 10 constants rather than three, with different fits made above and below a temperature of 20 °C, to give a piecewise fit, referred to by A&M as a "bicubic expression".

Absorption by specific chemicals

Some molecules within the seawater have more than one stable state, and changes from one to another are dependent on pressure. These changes can convert the energy associated with the fluctuating acoustic pressure into heat. This is described in Kinsler & Frey as chemical relaxation. Different phase changes involve different reaction times, and this lag in the response can be characterised by a relaxation time or relaxation frequency. Much faster changes have little effect as the molecular changes are too slow, so these absorption terms only affect lower frequencies.

The two principal chemical components of the ocean which contribute such relaxation frequencies are boric acid (f₁), and magnesium sulphate (f₂).

A&M give the following equations for these relaxation frequencies

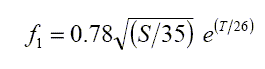
	kHz, Boric acid
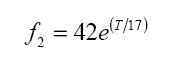
	kHz, Magnesium sulphate

Both f₁ & f₂ depend on temperature T, but only f₁, the boric acid frequency, depends significantly on the salinity S. Salinity is measured by the electrical conductivity associated with the ionic content, although most of the ions such as chlorine and sodium do not directly contribute to any absorption of sound. They do, however, provide strong attenuation of most electromagnetic waves such as radio communications.

The expression for f₁ is set around the typical seawater value of 35 parts per thousand (ppt), which is the default setting for the calculator, and the fixed value used by F&S.

The other parameter used to represent the nature of the seawater is the acidity or pH value. A typical ocean value adopted by F&S (first suggested by Lyman & Fleming) is pH = 8. This is a slightly alkaline solution, where the population of alkaline hydroxyl ions exceeds the acidic hydrogen ions. All oceans are somewhat alkaline with pH > 7, although there are concerns that this is being changed by the absorption of the excess atmospheric carbon dioxide associated with global warming.

The absorption due to a relaxation mechanism has a characteristic form

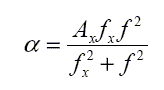
where A_x is a constant and f_x is a relaxation frequency.

A&M provide relatively simple expressions for the constants A_x associated with the two chemical relaxation terms to give a total

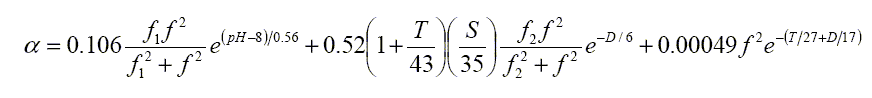
Ainslie and McColm Seawater Absorption Equation

dB/km

A&M note that whereas the acidity only affects the low frequency boric acid absorption, the salinity raises mid frequency absorption but decreases low frequency absorption. Temperature decreases absorption except close to the two relaxation frequencies.

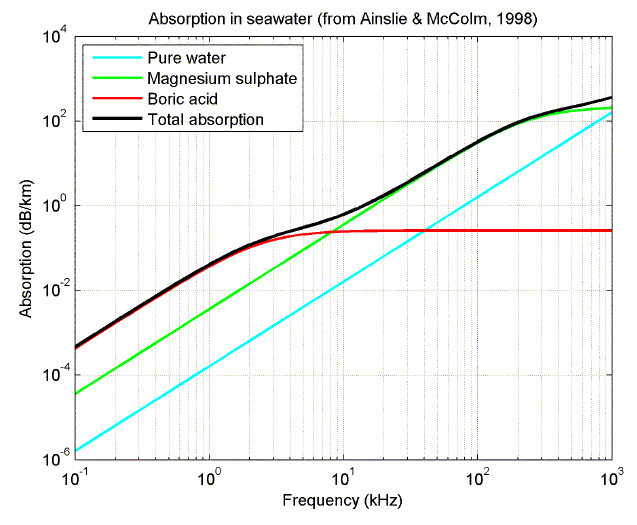
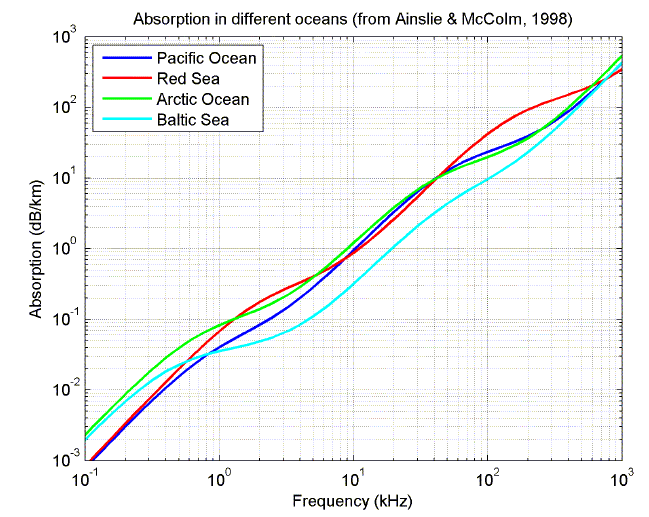
The following plots show the relative contribution from the different sources of absorption as a function of frequency, and the variation in total absorption with frequency for four different oceans (from Ainslie and McColm, 1998).

References

Ainslie M. A., McColm J. G., "A simplified formula for viscous and chemical absorption in sea water", Journal of the Acoustical Society of America, 103(3), 1671-1672, 1998.

Fisher F. H., Simmons V. P., "Sound absorption in seawater", Journal of the Acoustical Society of America, 62, 558-564, 1977.

Francois R. E., Garrison G. R., "Sound absorption based on ocean measurements: Part I:Pure water and magnesium sulfate contributions", Journal of the Acoustical Society of America, 72(3), 896-907, 1982.

Francois R. E., Garrison G. R., "Sound absorption based on ocean measurements: Part II:Boric acid contribution and equation for total absorption", Journal of the Acoustical Society of America, 72(6), 1879-1890, 1982.

Kinsler L. E., Frey A. R., Coppens A. B., Sanders J. V., "Fundamentals of Acoustics", Third Edition, Wiley, New York, 1982.

Any comments or suggestions about this model please contact Stephen Robinson