
|
| Adobe Acrobat Version (374 KB) |
The sensitivity of a hydrophone is often specified as the end-of-cable open-circuit sensitivity. This is the sensitivity of the hydrophone at the end of its cable when not connected to an electrical load. When a specific electrical load, such as an oscilloscope, an amplifier or extra cable is used at the output of the hydrophone, the end-of-cable loaded sensitivity of the hydrophone at a given frequency may be related to the open-circuit sensitivity in the following ways:
Consider the general case in which the hydrophone is considered as a two-terminal network of complex impedance ZH connected to an electrical load of complex impedance ZL. The end-of-cable loaded sensitivity of the hydrophone, ML, when connected to the specified load is related to the end-of-cable open-circuit sensitivity, MO, by:
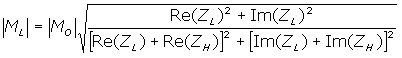
where Re and Im denote the real and imaginary parts of the
relevant complex impedance.
Often, as in the case of a preamplifier or oscilloscope input, the electrical load can be assumed to be a parallel combination of a resistance RL and capacitance CL. In this case, Re(ZL) and Im(ZL) are given by:
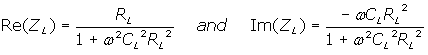
where ω is the angular frequency.
For hydrophones without an integral preamplifier, the effect on the sensitivity due to the addition of an extension cable can be calculated using the formula below. This formula requires complex impedance measurements of the hydrophone with extension cable and the extension cable alone in order to determine the change to the open-circuit sensitivity of the hydrophone caused by the addition of the extension cable.
The open-circuit sensitivity measured at the end of the extension cable, ML, can be derived from the open-circuit sensitivity of the hydrophone at the end of the integral hydrophone cable, MO, as follows:
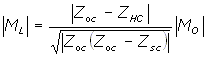
where:
ZHC is the complex impedance of the hydrophone and extension cable
ZOC is the complex impedance of the extension cable alone measured with the free ends open-circuit
ZSC is the complex impedance of the extension cable alone measured with the free ends short-circuit
A simplified correction is possible if the impedances of both the hydrophone and the load can be assumed to be purely capacitive. This is often a valid assumption for a hydrophone at frequencies much less than the resonance frequency and for loads such as extension cables.
If CH is the end-of-cable capacitance of the hydrophone (including any integral cable and connector) and CL is the capacitance of the load (e.g. the extension cable), the correction factor is calculated as below:
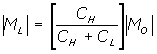
The low frequency, end-of-cable capacitance of a hydrophone is often quoted in the manufacturer's documentation and the capacitance of extension cable is usually specified in pF/m by the cable manufacturer. It is therefore possible to calculate an approximate sensitivity correction without the need for an impedance analyser or LCR meter.
Where it has been necessary to measure the electrical impedance of a hydrophone via an extension cable, the complex impedance of the hydrophone (with its integral cable) can be determined from further measurements of the complex impedance of the extension cable alone.
The complex impedance of the hydrophone (with its integral cable), ZH, is given by:
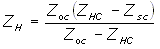
where:
ZHC is the complex impedance of the hydrophone and extension cable
ZOC is the complex impedance of the extension cable alone measured with the free ends open-circuit
ZSC is the complex impedance of the extension cable alone measured with the free ends short-circuit
For further information, contact Stephen
Robinson
| Press and media | Privacy Policy | Quality | HSE | Contact | Terms |
© National Physical Laboratory 2018
National Physical Laboratory | Hampton Road, Teddington, Middlesex, TW11 0LW | Tel: 020 8977 3222