Underwater Acoustics

The fundamental units for physical measurements are defined by the Systeme Internationale (SI). These underpin the commonly used acoustic decibel levels, by providing reference values (e.g. P_o), to generate the logarithmic ratios required.

Names of measured quantities and linking equations	Decibel formats (examples in the literature)	SI units + optional prefixes e.g. μPa (microPascal)	Comments
Sound pressure level (SPL) Acoustic pressure (P) SPL = 20 log (P/P_o)	dB re 1 μPa dB//μPa dB re 20 μPa	Pa (Pascal) - measured at a defined position - bandwidth must be specified for broadband sound	Note the different references for: - underwater (P_o = 1 μPa) - airborne (P_o = 20 μPa)
Sound power level (WL) Sound power (W) (in band B) WL = 10 log (W/W_o)	dB re 1 pW	W (Watt) pW (picoWatt, 10^-12 W)	Mainly used when describing airborne sound sources, usually over the whole audio bandwidth
Sound power spectrum level WSL = WL - 10 log B		W/Hz (Watt/Hertz)	Power per unit frequency can be measured for broadband sound
Sound pressure spectrum level	dB re μPa²/Hz dB re μPa/√Hz dB re 1 μPa in a 1Hz band	Pa²/Hz (Pa/√Hz is used for convenience, but is not a physical quantity)	Integration of broadband sound pressures gives the mean P² value, based on sound power
Sound intensity level (IL) Sound intensity (I) IL= 10 log (P²/Z)	dB re pW/m²	W/m² (Watt/square metre)	The airborne 0 dB reference level of 1 pW/m² is deemed to be the lowest audible level (at ~2 kHz)
Acoustic impedance (Z) Z = ρ· c		kg/(m²·s) or Rayl (Pa·m)²/W is a useful equivalent	The product of density ρ (kg/m³) and sound speed c (m/s)
Source level (SL) Source output (S) SL = 20 log (S/S_o) = 20 log ( P·r ) (P_o·r_o) = 20 log (P/P_o) + 20 log (r/r_o) = 20 log P + 20 log r (when P_o,r_o both unity)	dB re 1 μPa at 1m dB re 1 μPa·m dB re 1 μPa-m	Pa·m (Pascal·metre) Source output S should be - measured in a defined direction - have a specified bandwidth (except for single tones)	Source output S determines the power per unit solid angle, WA (watts per steradian). WA = S²/Z (see row above)

Analysis of transmission losses

Decibels are especially convenient for the analysis of transmission loss TL. This conveniently combines the exponential reduction of intensity due to absorption in the fluid, with the inverse square reduction of intensity due to spherical spreading. However, the reference distances must be kept consistent with the quantities used elsewhere.

This table only considers the spherical spreading of coherent signals in non reverberant conditions (i.e. no echoes). Other spreading models (e.g. cylindrical losses) can be applied to more complex environments.

Names of measured quantities and linking equations	Decibel formats (examples in the literature)	SI units + optional prefixes e.g. μPa (microPascal)	Comments
Absorption coefficient a a = 10 log (I₁/I₂) Intensity I₁ is reduced to I₂ by absorption over a distance r_o Absorption losses over range r, LA = a · r (losses are positive)	dB/m, dB/km, dB/kiloyard, The reference distance r_o is applied here in a different way to other decibel quantities. It is not "dB re 1m", but dB per m or dB/m	This is the attenuation in dB, over the reference distance r_o. Whilst attenuation is unitless, the absorption coefficient a has units of inverse distance (e.g. m^-1)	The attenuation due to absorption is an exponential decay. Doubling the distance doubles the decibel loss
Spherical spreading loss, LS (excluding absorption) LS = 20 log ( r / r_o) = SL - SPL	dB re 1m, dB//m A reference distance r_o must be defined to avoid ambiguity. The double slash provides a convenient short form	The reference is a distance r_o , usually given in m. This must be compatible with the ratio of S/P e.g. Pa·m/Pa	Doubling the distance divides the pressure by two,the intensity by four, and reduces the SPL by 6dB
Transmission Loss, TL TL = LS + LA = 20 log r + a r ( when r_o=1)	dB re 1m, dB//m NB: The inclusion of the exponential absorption term means that the normal rules are extended here	The reference distance r_o must be defined with extra care, given the complex relation, especially if r_o is defined differently for each term	The convenient way in which the decibel transmission loss covers both loss mechanisms is a major benefit, but can lead to serious errors

Some more examples of decibel quantities which sonar design engineers find useful, with their SI reference units

Names of measured quantities and linking equations	Decibel formats (examples in the literature)	SI units + optional prefixes e.g. μPa (microPascal)	Comments
Hydrophone receive voltage sensitivity (M)	dB re 1 V/μPa	V/Pa μV/Pa	Typical -206 dB re V/μPa or 50 μV/Pa
Transmit voltage response (TVR or S_V) from a source	dB re 1 μPa at 1m per Volt dB re 1 μPa·m/V	Pa·m/V	Typical 140 dB re 1 μPa·m/V or 10 Pa·m/V (for a piezosphere)
Transmit current response (S_I)	dB re 1 μPa at 1m per Amp dB re 1 µPa·m/A	Pa·m/A	The current response is significant for electrical matching and for reciprocity calibration
Power per unit solid angle		W/sr (Watts/steradian) A steradian is a unit solid angle which intercepts an area r² on a sphere of radius r, centred on the source	This helps to define directivity, and is given by the source output squared S² (Pa·m)², divided by the fluid acoustic impedance Z
Directivity index (DI) Directivity factor (D) DI = 10 log D	dB No reference unit is needed because D is a ratio	For a source: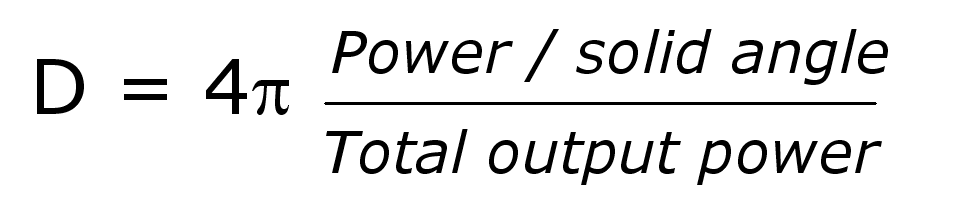	DI is also a simplified form of array gain, used to calculate signal/noise ratios of hydrophone arrays